ShareSoc
INVESTOR ACADEMY

Understanding Compound Interest

A sound understanding of compound interest significantly improves your ability to develop a successful investment strategy that suits you and to correctly evaluate potential investments. Examples of where such an understanding will help you are:

Calculating the rate of return or yield to maturity of bond investments
Understanding the sensitivity of investment returns to the return on capital employed (ROCE) that a business can achieve
The impact that an issue of bonds or preference shares by a business will have on the returns achieved by equity investors.
Calculating the annualised return your portfolio has achieved and/or working out when a desired target level of capital should be achieved.

In this chapter we explain:

What the term “compound interest” means
The impact of time on your expected returns
The impact of the interest rate on returns
Tools to help you with compound interest calculations, including a worked example of how a more sophisticated tool is used.

What is Compound Interest?

Simply put, compound interest is interest you earn on interest. For example, consider a bank savings account that pays 2% interest, compounded annually. After one year, an initial investment of £10,000 earns £200 of interest (2% of £10,000) – which means that the amount in the account at the start of the second year is £10,200. So, in the second year, the amount of interest earned will be £204, giving a closing balance of £10,404 (rather than the £10,400 which the account would have grown to, had only simple interest been earned).

The Effect of Time

Time is the investor’s friend. Holding an investment for longer has a much bigger impact on your returns than you would intuitively expect. The following chart shows how an initial lump sum of £10,000, earning 5% compound interest, grows over time.
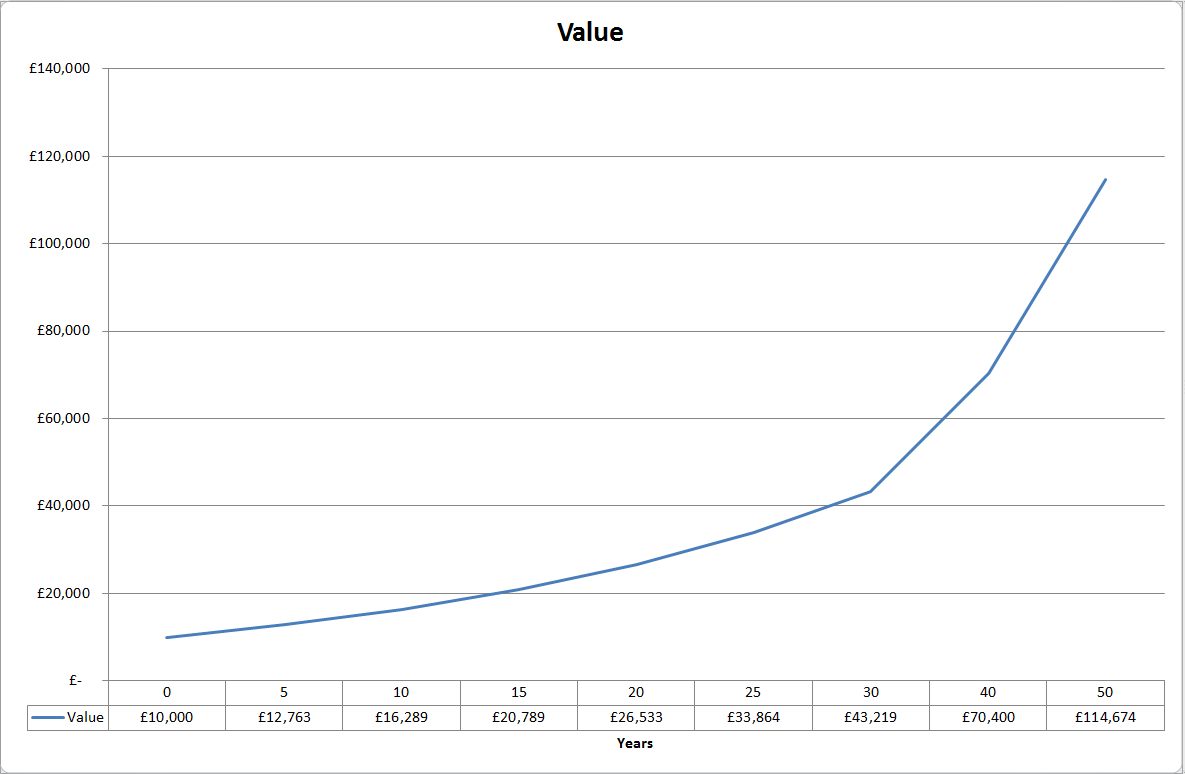
compoundingchart

Note how extending the amount of time the money is invested for by a relatively short period dramatically increases the final value obtained. This is a consequence of the geometric nature of compound interest.

The Effect of Interest Rates

Just as extending the duration of an investment has a disproportionate effect on returns, so do relatively small changes to interest rates earned. The following chart illustrates the effect of different interest rates on the ultimate value of an initial investment of £10,000 held for 20 years.

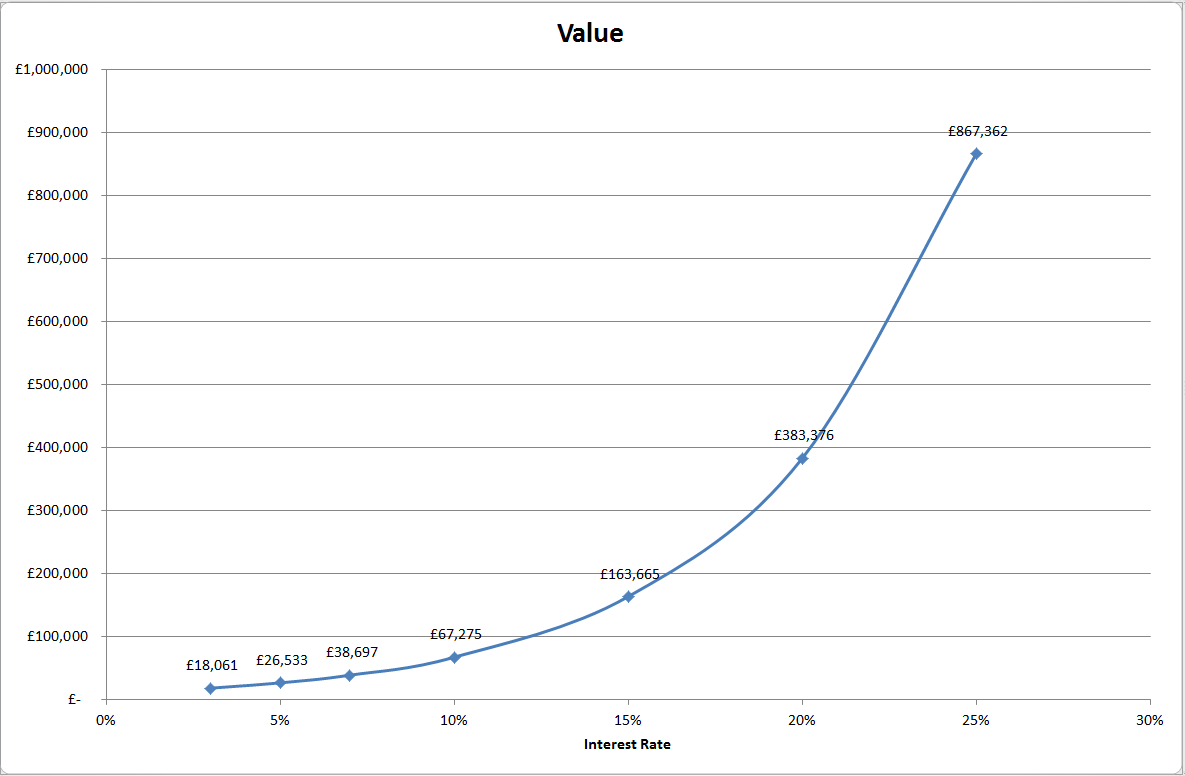
rateschart

Note once again how relatively modest changes to the interest rate have a dramatic effect on returns, over an extended period of time. E.g increasing the rate from 7% to 10% increases returns from £38,697 to £67,275, a 74% improvement. An important corollary to this is that the effect of charges by funds or advisers is disproportionate. E.g. if the underlying return on an investment is 10% but an annual fee of 1.5% reduces this to an actual return of 8.5%, instead of earning £67,275 you will earn £51,120 – a cost of £16,155 over the lifetime of the investment.

Compound Interest Calculation

There are many websites offering compound interest calculators. Here is an example of a nice simple one, that lets you calculate any of a number of types of result, given knowledge of the other relevant factors. E.g. given a target final sum and a known investment period, it can calculate the rate of return you’d need to achieve to reach that target.

All spreadsheet software offers a range of formulae to perform compound interest calculations. These are a vital part of the investor’s armoury and let you easily perform numerous analyses of the performance of your investments.

One of the most useful (but little known) functions in Excel for investment analysis is the XIRR function. It can be used to calculate the equivalent rate of return that a known/anticipated series of cashflows represents. Note that XIRR is built-in to Excel 2010 and later versions. In earlier versions, it is part of the (free) Analysis Toolpak, which must be added in before the function can be used.

The following Excel2010 spreadsheet illustrates how the XIRR function is used to perform a practical investment analysis.

DNA2DNA3.xlsx

This spreadsheet calculates the anticipated investment return of a specialist investment trust: Doric Nimrod Air Two (aka “DNA2”) [it also includes an equivalent worksheet for a similar trust, DNA3]. The DNA2 trust operates on a simple basis: it owns 7 Airbus A380 “superjumbo” aircraft, all of which are leased to the Emirates airline (one of the world’s largest airlines). Emirates operates the world’s largest fleet of A380s, totalling 75 aircraft.

Each aircraft is leased for a period of 12 years, and the leases are structured such that the regular lease payments are sufficient to:

a) Pay a dividend to investors in the trust

b) Fully repay debt finance (with interest) that DNA2 has taken on to purchase the aircraft. This debt is “amortising”, i.e. operates like a repayment mortgage with the debt repayments including both an interest and a capital component, and structured such that the debt will be fully repaid over the duration of the lease.

So, at the end of the lease terms, DNA2 will own the aircraft unencumbered by debt, and it is anticipated that the aircraft will be sold or otherwise disposed of, returning proceeds to investors in DNA2.

In the DNA2DNA3GRY sample spreadsheet, the entry in row 3 represents the current share price of DNA2 shares (in pence). Subsequent rows (4-34) represent regular dividend payments that the trust is expected to make (4.5p per quarter). The figures representing payments to investors are negative for XIRR to work, with the initial investment (i.e. the share purchase) being a positive number. Note that the (apparently attractive) simple annual yield on the trust at the price of 220p is 4*4.5 (=18)/220 = 8.2%… but this is not the whole story. What you need to know as an investor is the “gross redemption yield” (GRY) that can be expected from DNA2, i.e. what the compound rate of return on your money is, if held to maturity when the aircraft are ultimately sold.

A major factor in establishing the GRY is the anticipated sum that will be received when the aircraft are ultimately sold. DNA2 have commissioned 3 independent specialist valuers to provide an estimate of this each year – but note that this estimate is highly uncertain because there is not yet an established market for used A380 aircraft, given that the aircraft is a relatively new type.

Row 34 represents an estimate of the terminal value per share that shareholders will receive – note that both the precise date when this will be repaid, and the amount are uncertain and will depend on the market for the aircraft in 2025. The XIRR function in cell 1E uses:

The initial purchase price;
The regular dividend payments; and
The estimated terminal value

to calculate the equivalent GRY for the purchase of shares in the trust. By changing the estimated terminal value and the final redemption date (both of which are uncertain), you can examine the sensitivity of the GRY to changes in those parameters and hence form a view of the attractiveness of the investment (and at what share price it would appear attractive to you).

Note that the dividend payments are not guaranteed, but have been paid as anticipated to date. It is hard to see a reason for them not to be paid, barring a collapse of the Emirates airline.

Mark Bentley

Group description:	SIGnet Taunton is a new group with around 10 keen members at present, with a range of investment styles and experience. We welcome new members.
Meeting Type/Venue:	In person meetings at a golf club near to the centre of Taunton.
Meeting Frequency/Timing:	We meet on the first Monday of every month at a golf club near to the centre of Taunton, 11am until 3pm with a lunch break.

Group description:	An online group for those who are new to investing, or have only been investing for a few years. Including topics such as: – What is a share or a bond, why and how to buy them. – Comparing funds, unit trusts, Investment trusts and exchange traded funds. – Portfolio management and diversification. – ISAs, pensions, SIPPS and how to save tax. – How terms such as PE ratio and dividend yield are used to value a share. – How to use technical analysis or charting.
Meeting Type/Venue:	Online using Zoom.
Meeting Frequency/Timing:	Meetings are usually held on the last Monday of the month at 7:00pm.

Group description:	An online group for those who already have some experience in investing. Covering topics such as finding companies to invest in, financial statements and ratios, valuation / margin of safety, analysis of companies and investment trusts and exchange traded funds.
Meeting Type/Venue:	Online using Zoom.
Meeting Frequency/Timing:	Meetings are usually held on the last Wednesday of the month at 7:00pm.

Group description:	The Equity Income Group welcomes investors of all levels of experience, from beginners to advanced. The focus of meetings is on dividend paying Investment Trusts, though there is also discussion around individual shares.
Meeting Type/Venue:	Meetings are held online.
Meeting Frequency/Timing:	Meetings are held every 6 weeks on a weekday between 7 and 8:30pm.

Group description:	The Group welcomes investors of all levels of experience, from beginners to advanced. The focus of meetings is on all types of income generating financial instruments, from stocks through Trusts and Funds and ETFs to retail bonds. Meetings involve presentations from members, who are also expected to lead discussions from time to time, as well as discussions on what has been bought and sold since the last meeting.
Meeting Type/Venue:	Meetings are in-person in a venue in Central London.
Meeting Frequency/Timing:	Meetings are usually held on the last Thursday of every other month, starting with an informal lunch around 1pm followed by discussions until around 5pm.

Group description:	A welcoming group open to all types of investors. Typical meeting content is to have a deep dive presentation on a topic selected by the participants and a session on buy/ sell/ key lessons learnt last month.
Meeting Type/Venue:	In person at a friendly pub close to Piccadilly Circus
Meeting Frequency/Timing:	Monthly during the evening on the first Wednesday of the month.

Group description:	Our group is a broad church that contains investors of varying experience. Our members’ backgrounds are diverse and include corporate banking, engineering, teaching and the leisure industry. We generally pick a discussion topic for every meeting, e.g. housebuilders or the defence industry, and members are invited to research and discuss different aspects or companies within that industry. We also discuss stocks and investment trusts that we have bought, sold or are interested in and the reasons behind our decisions, and try to make sense of the ever changing investment environment. Discussions are robust and challenging but we are a friendly and approachable group who welcome investors of all levels – we just ask that you contribute, at whatever level you can.
Meeting Type/Venue:	Our meetings are held in a private room at a nice pub near to South Ealing tube station (Piccadilly Line), not far from Ealing Broadway (District, Central and Elizabeth Line).
Meeting Frequency/Timing:	We meet every 2 months, usually on a Wednesday morning at 11am.

Group description:	All levels of experience welcome. A typical meeting agenda includes: – Macro Environment – Trades: Members review existing positions and identify securities with promising TA entry patterns or setups and with suitable risk/reward. Any security, long, short, futures, options may be considered. The convener takes actual positions in trades and maintains his own detailed ledger, accurately measuring performance of individual securities and cumulative activity. Members are notified by e-mail prior to the entries or exits that are decided upon. Following each meeting an updated copy of the ledger is circulated together with the next meeting agenda. Members may wish to maintain similar ledgers of their own but there is no obligation to do so. – Technical Analysis: Techniques and systems used in trades. Members can request discussion of particular aspects of TA.
Meeting Type/Venue:	Online via Zoom
Meeting Frequency/Timing:	The first Tuesday of every month from 7 to 9pm

Group description:	Open to all investors / people with an interest in investing. Typical meeting will involve members talking about recent purchases, successes, failures and possible future purchases. Also with occasional visiting speakers or members making presentations on a topic of interest.
Meeting Type/Venue:	We aim to meet on the last Tuesday of each month in a private room at a pub in Playhatch. Start time 7pm with members encouraged to meet up around 6pm for a bite to eat / drink before hand, if their diaries allow.
Meeting Frequency/Timing:	7pm on the last Tuesday of the month. Meetings likely to last about two hours but with informal ‘overspill’ before / after.